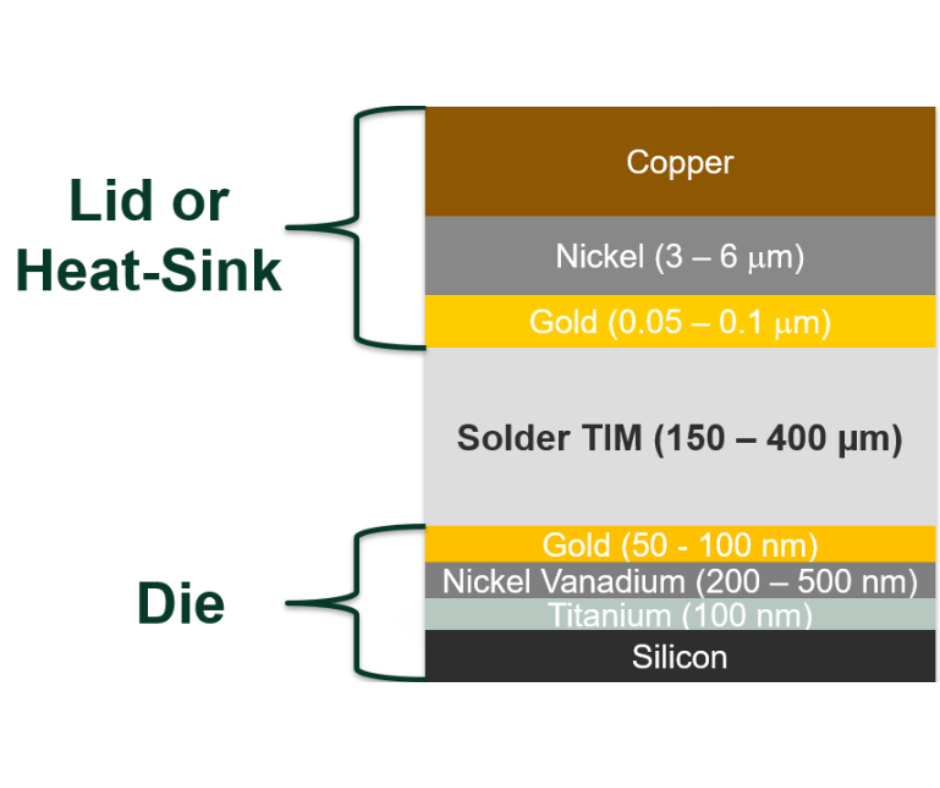
Folks,
Can it be almost 20 years ago that I developed the solder alloy density calculator? I have received more requests on this topic than any other. It surprises most people that the formula for calculating an alloy density is as in Figure 1 below:
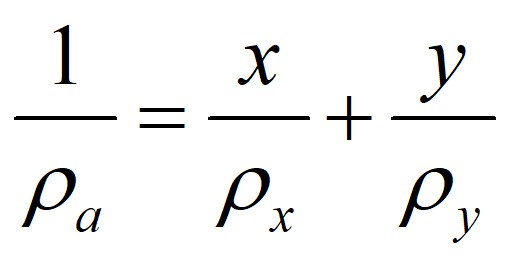
Figure 1. The formula for the density of an alloy.
Where ra is the alloy density, rx is metal x density, ry is metal y density, x is the mass fraction of metal x, and y is the mass fraction of metal y.
There has also been some interest in going in the other direction:that is, calculating the mass fractions of the metals in an alloy. This calculation can only be performed for alloys with two metals. The formulafor the mass fraction of metal x is in Figure 2 below:
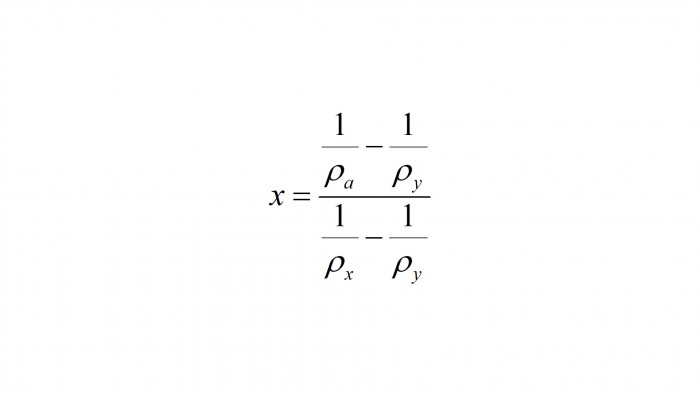
Figure 2. The formula for mass fraction x.
The equation in Figure 2 requires knowing the density of the alloy. A simple way to determine the density is to use the wet gold technique. This technique is discussed in a video that my good friend Phil Zarrow made a few years ago.
I explained how this technique works in apast post.Essentially, one weighs a sample of the gold alloy; let’s say it weighs 30 grams.One then weighs the sample as it is suspended in water (hence the term “wet gold”). This wet weight might be 27 grams. The sample will weigh less in the water because the water pushes up on it with a buoyancy force equal to the weight of the volume of water displaced.Dividing the difference between the dry and wet weights by the density of water (which is 1, so it makes it easy), one gets the volume of the alloy.Since the weight (mass) of the alloy and volume are now known, the alloy’s density can be calculated.In the case above, the density would be 30/(30-27) = 10 g/cc.This approach requires the type of hanging scale that is used to measure the weight of fish.Let’s call this approach "Wet Gold Technique I". See Figure 3.
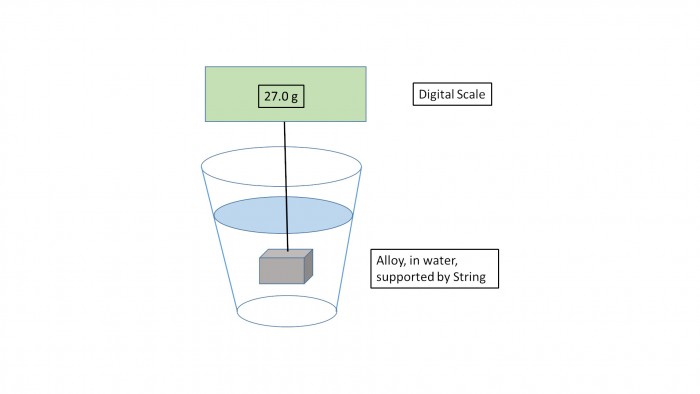
Figure 3. The Wet Gold Itechnique.
Avariant of this approach(Wet Gold Technique II) uses a lab-type scale.This second approach is often used in the field to measure the percentage of gold in gold silicate ores. So, after we measure the weight of our sample at 30 grams, we then put a beaker of water on our scale and zero the scale. We then suspend the sample in the water with a string. When the sample is submerged, we read 3 grams on the scale. This is the volume of water displaced, which is the same as the volume of the sample. Since water has a density of one g/cc, the volume of the water is 3.0 g/1g/cc = 3.0 cc. Therefore, the density of our sample is 30 g/3.0 cc = 10.0 g/cc.
I developed an Excel® (what would I do without Excel®?) spreadsheet to calculate the mass fraction metals in a binary alloy. Let’s assume our alloy is scrap jewelry gold (gold/copper). See Figure 4.
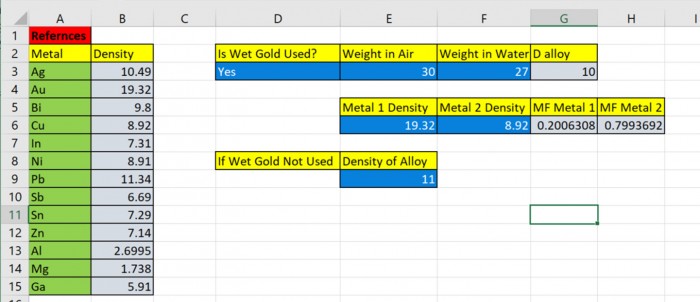
Figure 4. The Metal Mass Fraction Calculator
The spreadsheet is set up for Wet Gold Technique I. In cell D3, enter “Yes,” in cell E3, “30,” in cell F3, “27." Metal 1 is gold, so enter “19.32” in cell E6 and “8.92” in cell F6 for the density of copper. Read the weight fraction of gold as 0.2006 in cell G6 and of copper in H6 at 0.7994.
If Wet Gold Technique II is used, enter “No” in cell D3 and then enter the density in cell E9.
If you are interested in a copy of this Metal Mass Fraction Calculator, send me an email at [email protected].
Cheers,
Dr. Ron