Use FMEA to Manage Tin Whisker Risk

A tin whisker shorting betweenthe tin-plated terminal of an electromagnetic relay. Image courtesy of the NASA Electronic Parts & Packaging (NEPP) Program, https://nepp.nasa.gov/whisker.

Folks,

People rightly claim that we don’t thoroughly understand tin whiskers. They correctly point out that, even with mitigation, we can’t be certain that we can eliminate them. In addition, studies have shown that coatings to prevent tin whiskers don’t always work.

So does this seemingly unsettling situation give us less hope than Scrooge felt when confronted with the ghost of Christmas future? Most certainly not, if we look into the situation in a bit more detail.

While it is true that we don’t thoroughly understand tin whiskers, there is almost nothing that we DO thoroughly understand. When I worked at IBM and we discovered some new failure mode, one senior manager commented that if you can increase the number of those type of fails and also make the fails go away you have a quite good practical understanding of the phenomenon. This situation is basically true for tin whiskers. Tin whiskers typical form in tin platings over copper. Compressive stresses in the tin have been shown to be a major cause of tin whiskers (see Figure 1). These compressive stresses can arise from copper-tin intermetallic formation (1a), differences in thermal coefficient of expansion (1b), corrosion stresses (1c), and mechanical stresses (1d).

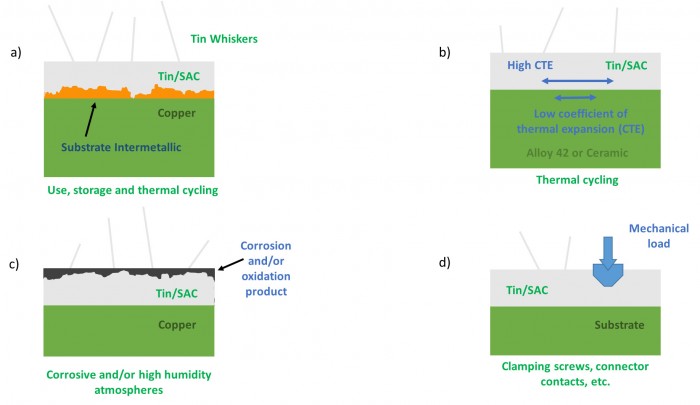
Figure 1. Some of the causes of tin whiskers driven by compressive stresses in the tin.

Increasing the compressive stresses dramatically increases tin whisker formation, while reducing these stresses dramatically reduces tin whisker formation.

To give a quantitative sense of tin whisker occurrence, Xu, Zhang, Fan, Abys, et al. [i] developed a Whisker Index (WI), defined as:

WI = Sn*d*L*f(L)

to measure the propensity to produce whiskers, where S is the area; n is the number of whiskers per unit area; d is whisker diameter; L is the whisker length; and f(L) is a non-linear function of length, that being 1 for a whisker length of 1 micrometer and 500 for a whisker length of 50 micrometers. Using this metric, they demonstrated quantitatively that compressive stresses are a major driving force in tin whisker formation. Consistent with the compressive stress driving force theory, these researchers showed that bright tin platings tend to have WIs in the 100,000 range, whereas simply changing to satin bright plating reduces the WI index to less than 10. Additionally, large grains in the tin plating are associated with low stresses, as is a matte or satin finish, so large grains are another positive indicator for mitigating tin whiskers. This situation does not even consider the additional tin whisker reduction that would occur by adding a thin nickel flash between the copper and tin or adding 2% bismuth to the tin.

To be fair, however, we can’t assume that these types of mitigation approaches will completely eliminate tin whiskers for the decades that some mission critical products must serve.

Coatings have been shown to provide considerable mitigation benefit, although most coatings may be penetrated by tin whiskers, parylene likely being the exception. However, to be a threat the tin whisker must penetrate the coating twice, as shown in Figure 2 below. In most cases, as it grows out from its base it will not have the stiffness to make the second penetration. Cases where double penetration have occurred have almost always been where the coating coverage is spotty.

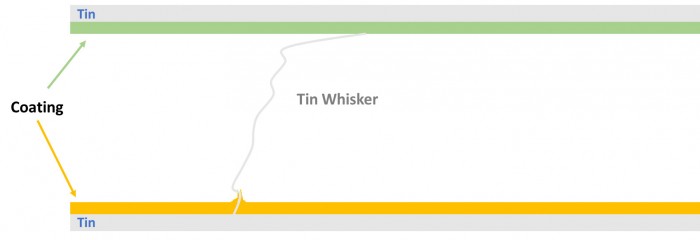
Figure 2. A tin whisker might easily penetrate the coating at its base, but to be a threat it must penetrate a second coating. At the second coating the whisker is long, weak and "floppy" and would have difficulty making the second penetration.

Failure modes and effects analysis (FMEA) is a good strategy to assess tin whisker risk. The central metric of FMEA is the risk priority number (RPN). For tin whiskers, the RPN is equal to the product of: (1) the probability of tin whiskers (P); (2) the severity, if a tin whisker exists (S); and (3) how hard it is to detect a tin whisker (D).  In equation form:

RPN = P*S*D

As a first example, consider a consumer product, like a mobile phone with a life of 5 years. With mitigation, on a scale of 1 to 10, P might be 2. For S, we might rate at a 3, as a failure in the device is unlikely to cause severe harm to anyone. Detection (D) is a problem because the tin whiskers that form later cannot be detected during manufacturing; hence, we would have to rate D as a 10. So, the RPN is: 2*3*10 = 60, which is not too high. Therefore, with P and S at relatively low values, a tin whisker mitigation strategy would likely be successful for any consumer product. It should be pointed out that determining the RPN numbers would almost certainly require supporting data, brainstorming sessions, and a buy-in from the entire product team. The team would also have to determine any appropriate mitigation strategy such as avoiding bright tin coatings on component leads and perhaps using a flash of nickel between the copper and the tin.

Now consider a mission critical product, such as certain types of military equipment. If we assume that the electronics have a service life of 40 years and that a failure could cause bodily harm or death, we could likely end up with a consensus that RPN = 10*10*10 =1000, the highest RPN possible. This situation would demand that special tactics be used to address the tin whisker risk. These tactics will be discussed in my paper and presentation to be given at SMTA Pan Pacific 2019. I hope you can join me!

Cheers,

Dr. Ron