Folks,
Let’s look in on a graduate student of Ivy University…
John Foster felt very fortunate. Not only did he get his undergraduate degree summa cum laude, but was now a graduate student at Ivy Universityunder the tutelage of the famous Professor Patty Coleman. While contemplating these pleasant thoughts, he was working on his homework in advanced statistics when Professor Coleman walked up to his desk.
“Hey, John, I have a little assignment for you. Mike Madigan, CEO of ACME, has a vendor that is guaranteeing zero defects in lots of diodes that ACME buys, yet when ACME gets the lots they find a defect rate of around 1% or more. Can you contact ACME’s quality engineer, Frank Ianonne, to see how you can help?" Patty asked. “We covered this topic in the intro stats class you took last term,” she finished.
“Sure, glad to help,” replied John.
“Thanks, I’m going to SMTA’s PanPac for the first time and have a lot going on there,” Patty said thankfully.
“Wow,” John thought, “the pressure is on.”
John contacted Frank and learned that the vendor’s sales engineer, Mike Gladstone, said that they sample 20 diodes from each 10,000-part lot. If they find no defects in in the sample of 20, they claim they can say that there are 0 defects with 95% confidence, since 19 out of 20 is 95% and they found no defects.
“Yikes,” John thought, “this can’t be right.”
He thought about this and finally came up with what he confidently feltwas the answer, especially after looking at his notes from the class Professor Coleman mentioned. He contacted Frank and they set up Zoom call with Mike to discuss the issue.
On the Zoom call after introductions, Frank asked Mike how they determine that a lot has zero defects.
“I’m glad to have the opportunity to explain this to youse guys,” said Mike.
It seemed to John that his tone was arrogant.
Mike continued, “Well, you will agree that 19 out of 20 is 95%, right?”
“Yes,” responded Frank and John.
“So, if we don’t get no defects in 20 samples, we got zero defects in the lot with 95% confidence. If we had one defect in the 20 samples, we couldn’t claim to have no zero defects in the lot,” Mike said.
“Mike, look at the image I took of one defect (a red bead) out of 2000 beads." (See Figure 1.) "If I selected 20 beads on the leftside of the container, how would I know that the defect rate is 0.0005 (1 in 2000)?” asked John.

Figure 1. The red bead is one “defect” out of 2000.
There was long silence.
“Mike what is your answer?” asked Frank.
Still no answer.
“The answer is that the only way you can assure zero defects is to evaluateall of the samples,” said John.
“You’re just confusing the issue with that there photo,” Mike spit out.
“Seems quite clear to me,” said Frank.
“You Ivy League types is all the same. You confuse the issue with mumbo jumbo when any dufuss can see I’m right,” Mike screamed.
Some profanity followed and Frank cut Mike’s Zoom feed.
“I see your point John,” Frank said. “but, can you give me some math to back it up?”
“Sure,” John replied.
“Let’s consider a case where the defect rate is not zero, but quite low, say 1 in 10,000 in a very large population. When we select the first sample, the likelihood of it being good is 0.9999 (10,000-1)/10000). What is the likelihood that the second one will be good?” John asked.
“Ah, let’s see…0.9999, right?” Frank answered.
“But what is the likelihood of both events?” John asked.
“Wait, I remember from a statistics class I took a few years ago, it’s 0.9999 x 0.9999,” Frank said triumphantly.
“And the likelihood of three in a row being good?” John asked again.
“0.99993,” Frank answered confidently.
“So let’s say we sample so many times, let’s call it n times, that 0.9999n = 0.05. What does this tell us?” asked John.
“Hmm, ………,” replied Frank.
“Well, how likely is this to happen if the defect rate is 1 in 10,000?" John asked.
“Wait, I see, it would only happen 0.05 or 5% of the time.” Frank responded excitedly.
“So, let’s say we didn’t know the defect rate, what could we say if we sampled n and got no defects?” queried John.
Frank was stumped.
“I’ll tell you what, think about it and we will get back tomorrow. It's already almost 6PM. Oh, and see if you can calculate what n is. Let’s Zoom at 10AM," John proposed.
Time flew quickly and John and Frank were Zooming again.
“John, you just about killed me, I had trouble sleeping, but I think I have it after reviewing my stats book and doing some Youtubing,” Frank began.
“Well, if we didn’t know the defect rate and wanted to see if it was at least as good as 1 in 10,000 and we sampled n such that 0.9999n = 0.05, we could say with 0.95 (1 – 0.05) confidence that the defect rate was 1 in 10,000 or less,” Frank said triumphantly.
“Precisely,” John exclaimed.
“But what is n?” John asked.
“That’s where I am stuck. We have the equation 0.9999n = 0.05, but I can’t solve for n,” Frank said dejectedly.
“Hint: Logarithms,” John replied.
“That’s it, I got it,” said Frank enthusiastically.
Frank worked for a few minutes with a calculator, and came up with the solution in Figure 2.
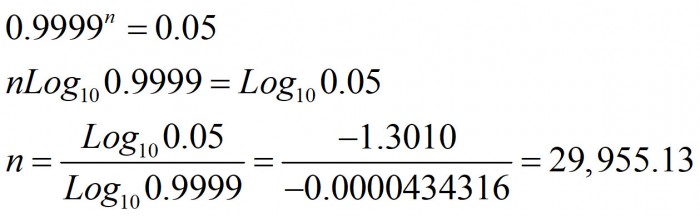
Figure 2. The Defects Calculation
“So, to show with 95% confidence that the defect rate is 1 in 10,000 or less, we would have to sample almost 30,000 components and find no defects,” Frank exclaimed.
“By looking at the equation, you can see if the defect rate was zero, 0.9999 would be replaced by 1 and the log of 1 is 0 so you would need an infinite sample,” said John.
“So, the only way to show 0 defects is to sample all of the components,” Frank said.
“Right!” replied John.
Cheers,
Dr. Ron