Folks,
As Patty was walking past the Professor’s office on her way to see Pete and Rob, she decided to drop in.
“Professor, I got the strangest phone call … a man claimed he had invented a machine that could create energy,” Patty began.
“Tell me about it,” the Professor chuckled.
“Well, he correctly noted that, when he took his kids to the beach, a submerged beach ball pushed up with a lot of force. So, he developed a technique to extract the energy produced when the ball is released,” Patty explained.
“Let me guess,” the Professor offered. “He then developed a technique to continuously extract energy; an energy producer of sorts.”
“Exactly! How did you know?” Patty responded.
“Well, I have been here about 40 years, and I have had forty such calls,” the Professor said.
“Tell me the details of your call,” he continued.
“There would be a box of small mass with a geneartor and pump inside; the generator and pump occupying little of the volume of the box.The boxwould be filled with water at the top of a lake and would thenwould sink to the bottom. Once thebox was at the bottom, the water would be pumped out and the buoyancy would cause the box to rise. A rope would guide the box on its up and downjourney and the generator would spin as it travels up the rope, hence generating electricty. The cycle would be repeated over and over and, in a sense, become a power plant,” Patty explained.
“And the problems are?” the Professor asked.
“I told him that it violates the laws of thermodynamics, and that I could make some calculations that would show that it would not work. Basically, the amount of energy required to pump the water out is greater than what the buoyancy would generate, considering friction etc,” Patty replied.
“His response?” the Professor led.
“My sense is that he thought he could make it work, in spite of the physics,” Patty answered.
“In my experience, that is always the response. Probablymy most troubling experience was a chap who convinced a small venture capital firm to advance him about $3M. He had a machine that, he claimed, continuosly extractedenergy out of the earth’s magnetic field. The biggest shock to me was that the leader of the venture capital firm was a graduate engineer who had retired as COO of a Fortune 50 company. I still haven’t figured out how such an accomplished person could not see that an energy-producing machine is not possible,” the Professor expounded.
“What was the upshot of all of this?” Patty asked.
“Well, they didn’t pay my consulting fee when I explained how it couldn’t work,” he chuckled. I checked a few months ago and the company’s website is down,” the Professor replied.
“The people that are into this folly don’t even realize that, if an energy-creating machine could be made, it would be the greatest discovery in history,” the Professor went on.
After a few more minutes of this discussion, Patty resumed her short walk to Pete’s office. Rob was already there.
“Looks like Mike Madigan needs us again. Did you see the email he sent us?” Pete asked.
“No, what’s up?” Patty and Rob said in unison.
“Something about Cpk,” Pete answered.
Patty reached for the phone to set up a conference call to Mike.
As she dialed, Patty admonished, “Now remember you two, good manners. No laughing at any of Mike’s questions.”
“Yes, ma'am,” Pete and Rob said in unison.
Mike’s secretary answered and said she would put them right through.
After a few pleasantries, Mike got to the point.
“Remember the tolerance analysis and specification that you did for passive resistor and capacitor length?” Mike began.
“Yes. We were all involved in that project,” Patty answered.
“So, it is a Cpk = 1, or a Three Sigma spec, right?” Mike asked.
“Sure,” Patty, Rob, and Pete answered in unison.
“So, what percent of parts should be out of spec?” Mike asked.
“Let’s see … Three Sigma is 99.73% of parts in spec … so that would be 0.27% out of spec,” Pete calculated.
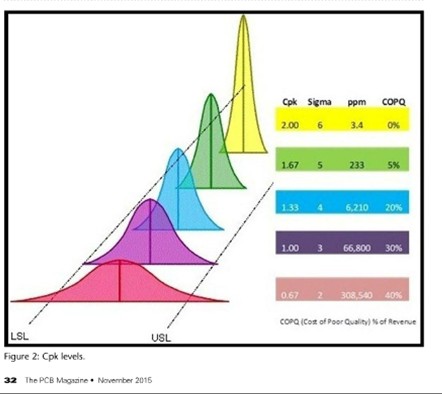
“Well, they are shipping us 5% out of spec parts and claiming they are better than Three Sigma, or a Cpk of 1, because they used a recently published graph, that said a Three Sigma, or Cpk = 1, process was 6.68% of parts out ot spec. I just sent it to all of you,” Mike said.
Pete opened the email and showed it to Patty and Rob.
“I’ll be darned! It does say that a Cpk = 1, or Three Sigma, has a defect rate of 66,800 defects per million or 6.68%,” Rob groaned.
“I’ll bet it has to do with the definition of ‘Six Sigma,’” Patty opined.
A look of recognition came over Pete and Robs eyes.
“What do you mean by the definition of ‘Six Sigma?’” Mike asked.
“We have all heard people claim that ‘Six Sigma’ is 3.4 ppm out of spec. Actually that’s a 4.5 sigma process. This definition allows a drift in the average of 1.5 Sigma that knocks the Cpk down to 1.5. True Six Sigma is a Cpk = 2 and is 0.002 ppm parts out of spec.” Patty replied.
“I’m a bit confused. But, let me show you some of the length data for 0402 passives,” Mike said.
“We measured them metrically so the length should be 1 mm +/- 0.1, Three Sigma. Instead, it is more like 1 mm +/- 0.1, Two Sigma. That’s a little more than 5% outside of the spec,” Mike continued.
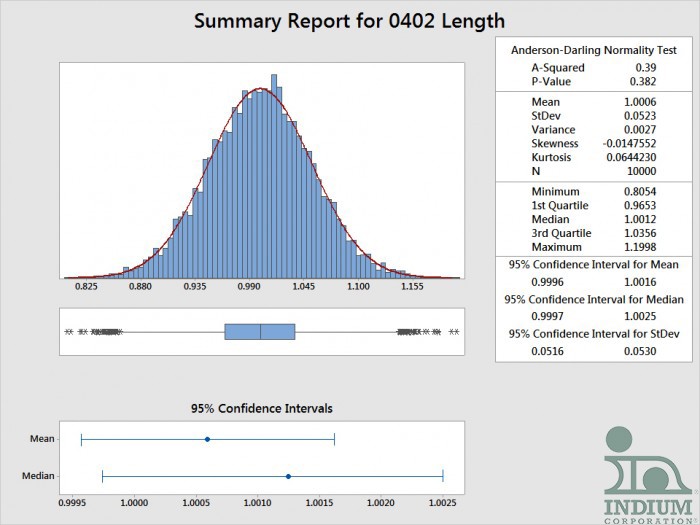
A Minitab Analysis of the 0402 Length Data.
“Give us some time to sort it out,” Patty suggested.
Is a Cpk of 1, or aThree Sigma, process really 66,800 ppm (6.68%) out of spec? Will Patty and the crew figure out what’s going on?
Stay tuned…
Cheers,
Dr. Ron